This humbling aspect of Pi is also a perfect metaphor for Learning – as a process of smoothing the corners and resulting in well-rounded individuals . It tells us that Learning is a continuous and never-ending journey, towards that unachievable perfection…. Thus Pi represents Learning – and in many ways, Pi represents, shall we say, Life itself!

Pi is arguably the most famous number in the world of Math. In Math, alphabets (English or Greek) are used to represent (yet) unknown numbers. There are typical letters used to represent specific types of unknowns (theta for angles, delta for small numbers, epsilon for very small numbers etc.). But Pi is among the very few that almost always represent just one number (called Pi).
We often assign Pi the values like 22/7, 3.14, 3.14159 etc. based on the exact application use case. But by definition, we do not know (and we cannot know) the precise value of Pi.
The simplest way to look at Pi is as the ratio of the circumference of a circle to its diameter. But that sounds simple – then why this mystery?
The mystery actually comes from the fact that we cannot have (and hence measure) a perfect circle! A perfect circle is an Utopian idea and what we create are just approximations of that idea. This now sounds mysterious and quite profound. Let us examine this further.
In dealing with curves like circles, a technique usually employed by Mathematicians is to ‘approximate’ the curve with a number of small straight lines. Thus a circle can be approximated by a polygon (square, hexagon etc.). So let us start with a square (picture). Then the circumference of our circle would correspond to the perimeter of the square and the diameter would be its diagonal. Now if you take the ratio of the perimeter to the diagonal, you would get the value to be 2.828. This is our first approximation for Pi – which is far from the value we know.
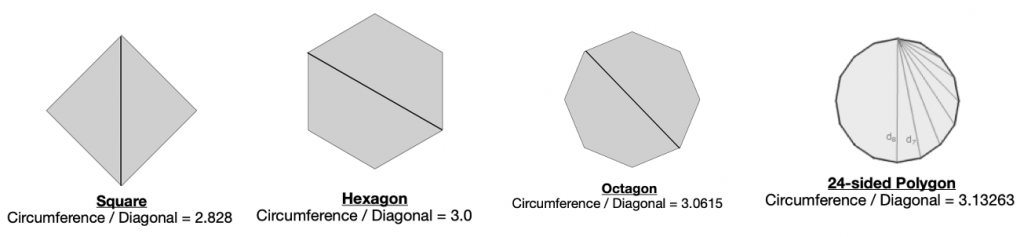
Now consider a hexagon (6 sides). In this case, the value of the ratio of the longest diagonal to the perimeter is 3.0. OK, now we have got something closer to our value of Pi, but still not good enough for any practical purposes.
Increasing the number of sides of the polygon to 8, 16, 24 etc., you can see that the ratio gets closer to our value of Pi. The table below summarizes this. You can also see that with 24 sides, the picture is visually pretty close to a circle. But to get a 5-digit accuracy, you have to go up to about 1000 sides!
But no matter how many sides you take for the polygon – you will never reach the perfect circle.
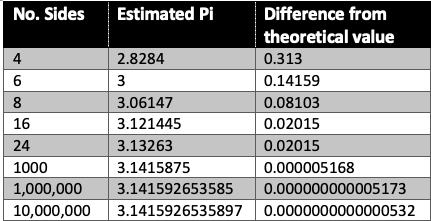
So what does this say about Pi? It is a number with unending decimal places, whose exact value can never be determined. The closer your approximation gets to the ideal circle, you have a more precise value.
In addition to this classical (geometric) approach, there is also a modern (analytical) approach developed to estimate the value of Pi. This consists of evaluating the circumference of a circle for a given diameter by applying finite series approximations to a slowly converging infinite series. This method was first used by Madhava (1350 AD) and his disciples of the famous Kerala School of Mathematics of the 14th to 16th centuries (Ref. below). For the learners, looking at Pi as the sum of an infinite series gives brilliant and direct insights to understanding the nature of this number – its infinite and unknowable nature.
In terms of applications, Pi broadly shows up in scenarios where a circle or a part of a circle is involved. This includes circular and spherical shapes, circular motions, waves, oscillatory motions, spiral motions, spiral shapes, cyclical changes etc. This makes it useful in a variety of practical scenarios.
The wide variety of application areas include AC Electric Power, Electronic communication, Rocket Science, DNA structures, shapes of River Basins, understanding of earthquakes etc.
Pi also appears in some scenarios where there is no obvious circular pattern involved – for example, in the distribution of Prime Numbers in the number system But some think that this indicates a deeper underlying aspect that we have not yet understood!. (Note: this should not be confused with the pi-function, which defines the number of prime numbers less than a given integer).
Pi reminds us that as we improve our tools and models, we get closer to the perfection of an idea (perfect circle) – but we could never reach that. This humbling aspect of Pi is also a perfect metaphor for learning – as a process of smoothing the corners and resulting in well-rounded individuals. It tells us that Learning is a continuous and never-ending journey towards that unachievable perfection.
Pi represents Learning – and in many ways, Pi represents, shall we say, Life itself!
Bibliography
“Chapter 10.” The Crest of the Peacock: Non-European Roots of Mathematics, by George Gheverghese Joseph, Princeton University Press, 2011.
Sankar is the founder and CEO of Silver Pi.
He had worked in Banking and Technology for about three decades before switching to Education. He is an Electrical Engineer by training, with a career in Technology and Banking across Japan, USA, Singapore and India.


Pingback: ‘Pi day’ Thoughts – Silver Pi Blog